SegmentTree

구간별로 특정한 결과 값을 관리할 때 사용하는 자료구조.
이진트리로 재귀적 구현이 특징.
- query (특정 구간의 결과) O(logN)
- replace (특정 인덱스 교체) O(logN)

 

안녕하세요 :) 오늘은 SegementTree에 대해 알아보려고 합니다.

먼저 SegemetTree 는 언제, 왜 사용할까요? 

SegemtTree 라는 이름이 나타내듯이 구간별로 특정한 결과값을 관리하고 싶을 때 사용하는 자료구조 입니다.

주로 구간 합을 구할 때 많이 사용하죠! 

세그먼트 트리는 이진트리로 leaf 노드가 해당 인덱스의 값을 가지고 있습니다.

아래 그림처럼 전체 구간부터 반씩 잘라서 구간을 나눠 놓은 자료구조에요!

세그먼트 트리의 핵심은 재귀적 반복에 있습니다. 생각보다 어렵지 않아요 :)

 

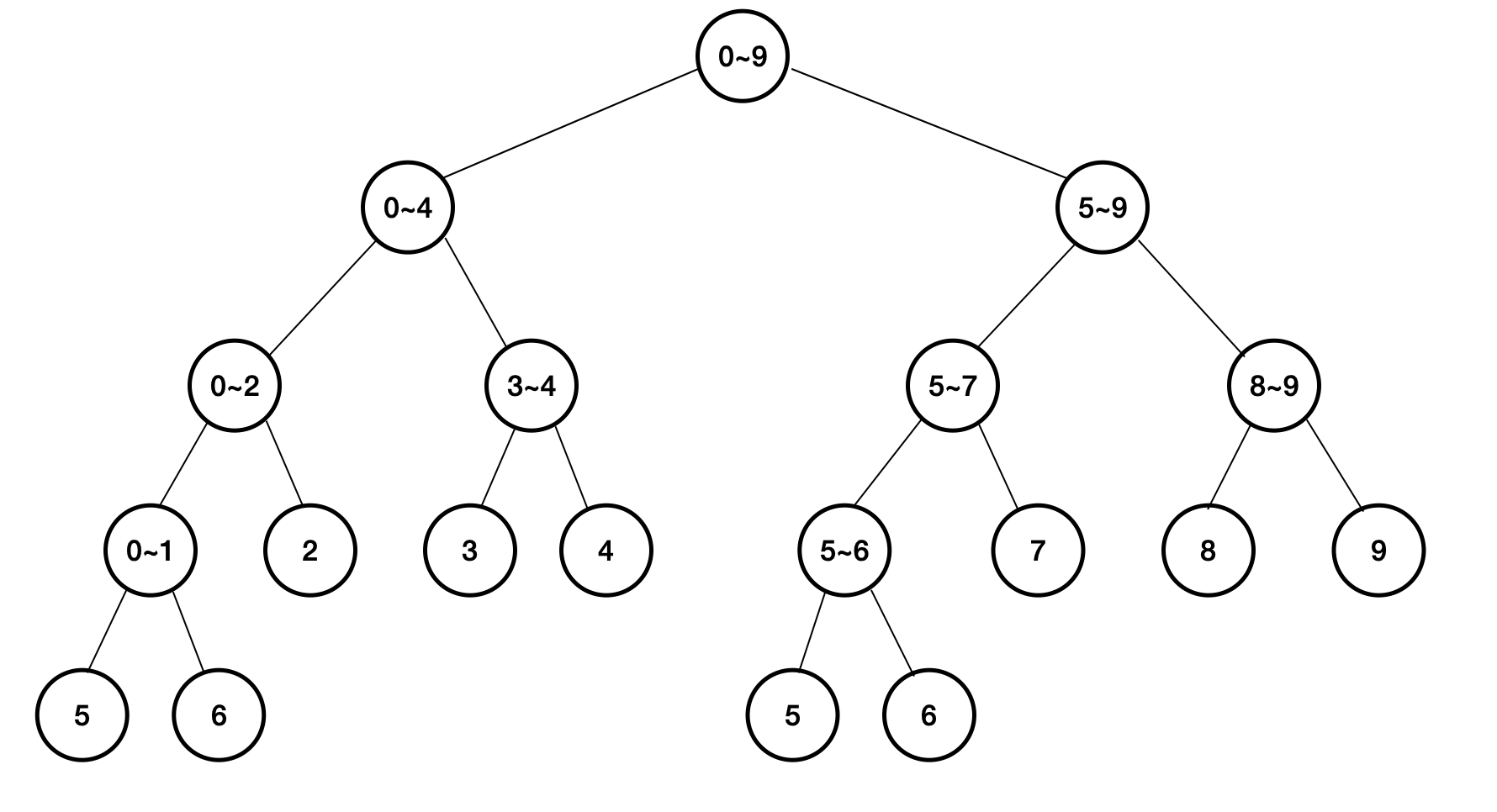
SegementTree 구성

먼저 트리의 형태부터 살펴볼게요. 트리의 각 노드에는 어떤 게 필요할까요? 

네 먼저 값, 구간, 자식노드들, 연산이 필요합니다!

class SegmentTree<T> {
  var value: T
  var function: (T, T) -> T
  var leftBounds: Int
  var rightBounds: Int
  var leftChild: SegmentTree<T>?
  var rightChild: SegmentTree<T>?
}

 

Init

먼저 배열을 입력 받아서 트리를 구성해보려고 해요.

세그먼트 트리의 구현은 재귀적으로 이루어집니다. 재귀의 핵심은 끝에 이루어질 기저사례죠! 

leftBounds == rightBounds 일 때가 leaf 노드가 될거에요.

아니라면 반을 나눠서 init 해주고 연산합니다 :)

init(array: [T], leftBounds: Int, rightBounds: Int, function: @escaping (T, T) -> T) {
    self.leftBounds = leftBounds
    self.rightBounds = rightBounds
    self.function = function
    
    if leftBounds == rightBounds {
    	// leaf
        self.value = array[leftBounds]
    } else {
        let middle = (leftBounds + rightBounds) / 2
        self.leftChild = SegmentTree<T>(
            array: array,
            leftBounds: leftBounds,
            rightBounds: middle,
            function: function
        )
        
        self.rightChild = SegmentTree<T>(
            array: array,
            leftBounds: middle+1,
            rightBounds: rightBounds,
            function: function
        )
        self.value = function(leftChild!.value, rightChild!.value)
    }
}

 

그냥 배열로 구성하려면 일일이 경계를 넣어줄 필요는 없겠죠? convience init도 만들어볼게요.

convenience init(array: [T], function: @escaping (T, T) -> T) {
    self.init(array: array, leftBounds: 0, rightBounds: array.count-1, function: function)
}

 

이렇게 간단하게 초기화가 가능합니다.

 

Query, 구간 결과 구하기

이제 원하는 구간의 값을 구해볼까해요. 

구간은 크게 4가지 경우가 될 수 있습니다. 

 

1. 구간과 정확하게 일치

구간과 정확히 일치하면 그냥 그 노드의 값이 찾는 결과가 됩니다.

// left, right가 모두 일치 -> 자기 value 리턴
if self.leftBounds == leftBounds, self.rightBounds == rightBounds {
    return value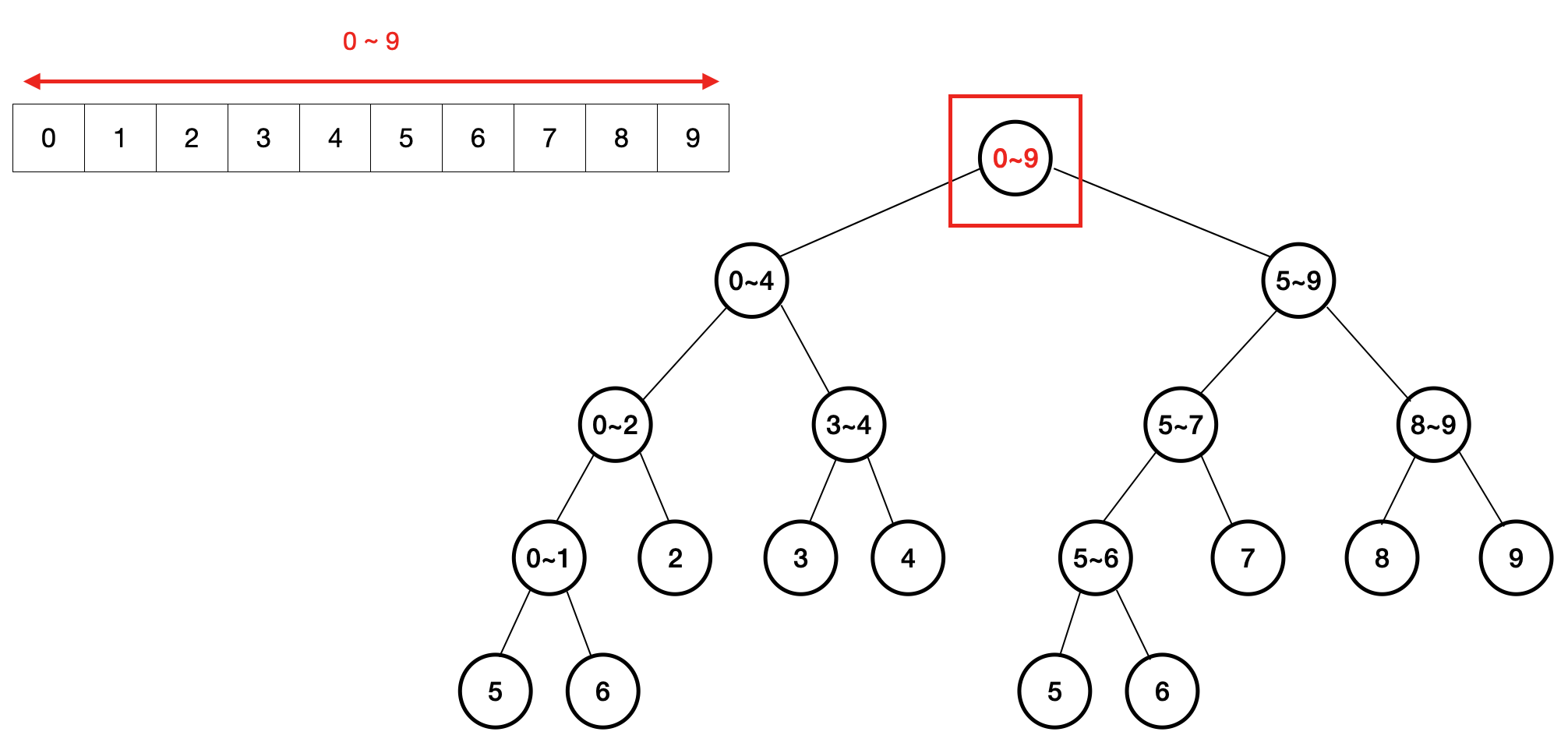
}

 

2. 오른쪽 구간에 포함

만약, 오른쪽 구간에만 포함된다면 오른쪽 자식 트리에서 다시 탐색을 시작합니다.

왼쪽 자식의 rightBounds 가 leftBounds 보다 크다면, 오른쪽에 있으니 오른쪽 자식에서 다시 탐색을 시작합니다.

// 왼쪽자식의 오른쪽이 left보다 작다. -> 오른쪽 자식에 모두 포함되므로 오른쪽부터 다시
if leftChild.rightBounds < leftBounds {
    return rightChild.query(withLeftBounds: leftBounds, rightBounds: rightBounds)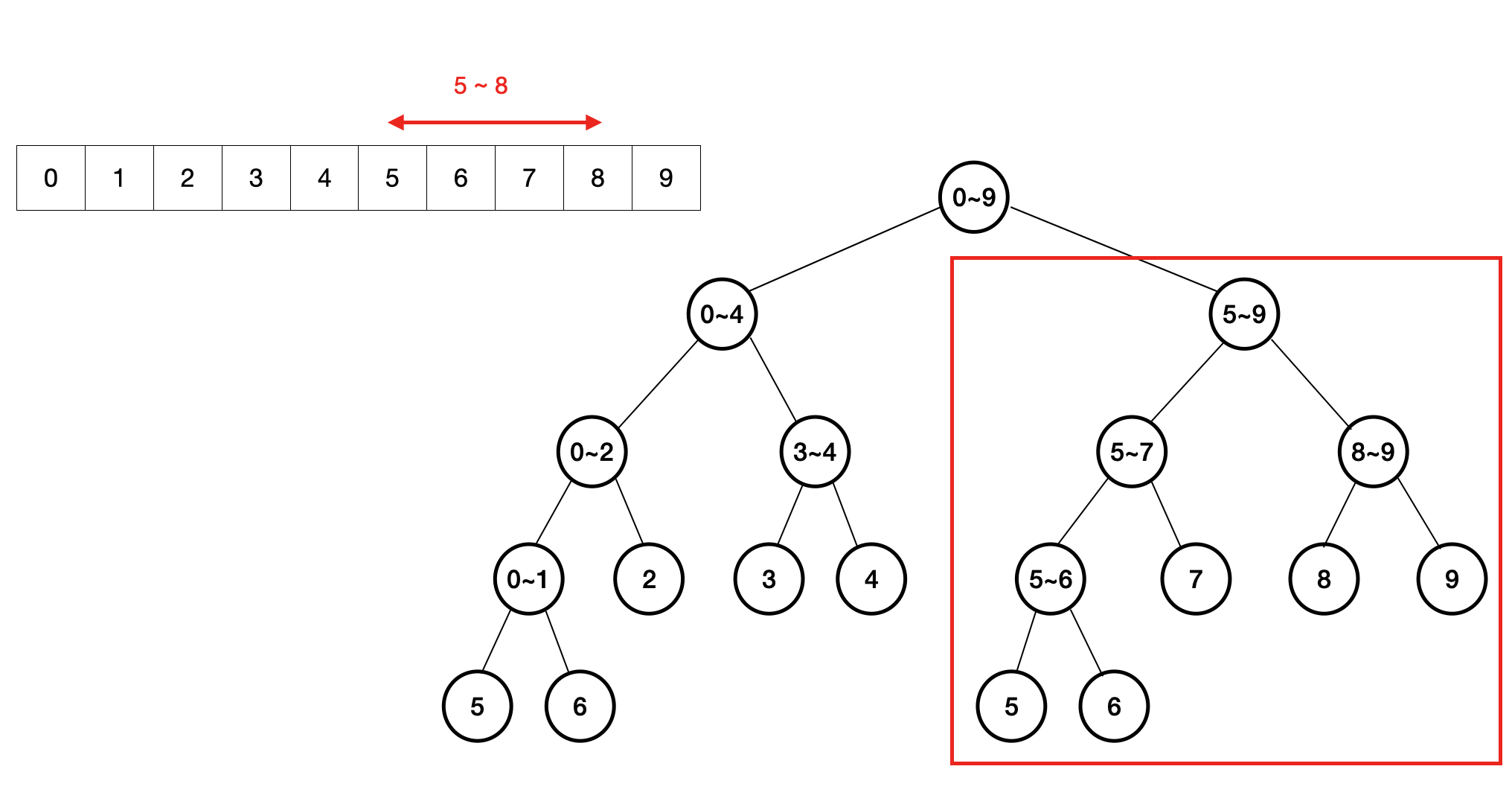
}

 

3. 왼쪽 구간에 포함

마찬가지로, 왼쪽 구간에만 포함된다면 왼쪽 자식 트리에서 다시 탐색을 시작합니다.

이번엔 오른쪽 자식의 leftBounds 가 rightBounds 보다 크다면, 왼쪽 자식에서 다시 탐색을 시작합니다.

// 오른쪽자식의 왼쪽이 right보다 크다. -> 왼쪽 자식에 모두 포함되므로 왼쪽부터 다시
else if rightChild.leftBounds > rightBounds {
    return leftChild.query(withLeftBounds: leftBounds, rightBounds: rightBounds)
}

 

4. (1, 2, 3이 아니라면) 양쪽 자식에 걸쳐있다.

1, 2, 3이 모두 아니라면 이제 양쪽 자식에 모두 걸쳐 있는 구간이 되겠네요, 

그렇다면 leftBounds 부터 왼쪽 자식의 오른쪽 끝까지,

그리고 오른쪽 자식의 왼쪽부터 rightBounds 까지의 

결과를 각각 구해서 연산해주면 됩니다!

// 양쪽 자식들에 걸쳐져 있음 -> (leftBounds ~ leftChild.right) + (rightChild.left ~ rightBounds)
else {
    let leftValue = leftChild.query(withLeftBounds: leftBounds, rightBounds: leftChild.rightBounds)
    let rightValue = rightChild.query(withLeftBounds: rightChild.leftBounds, rightBounds: rightBounds)
    return function(leftValue, rightValue)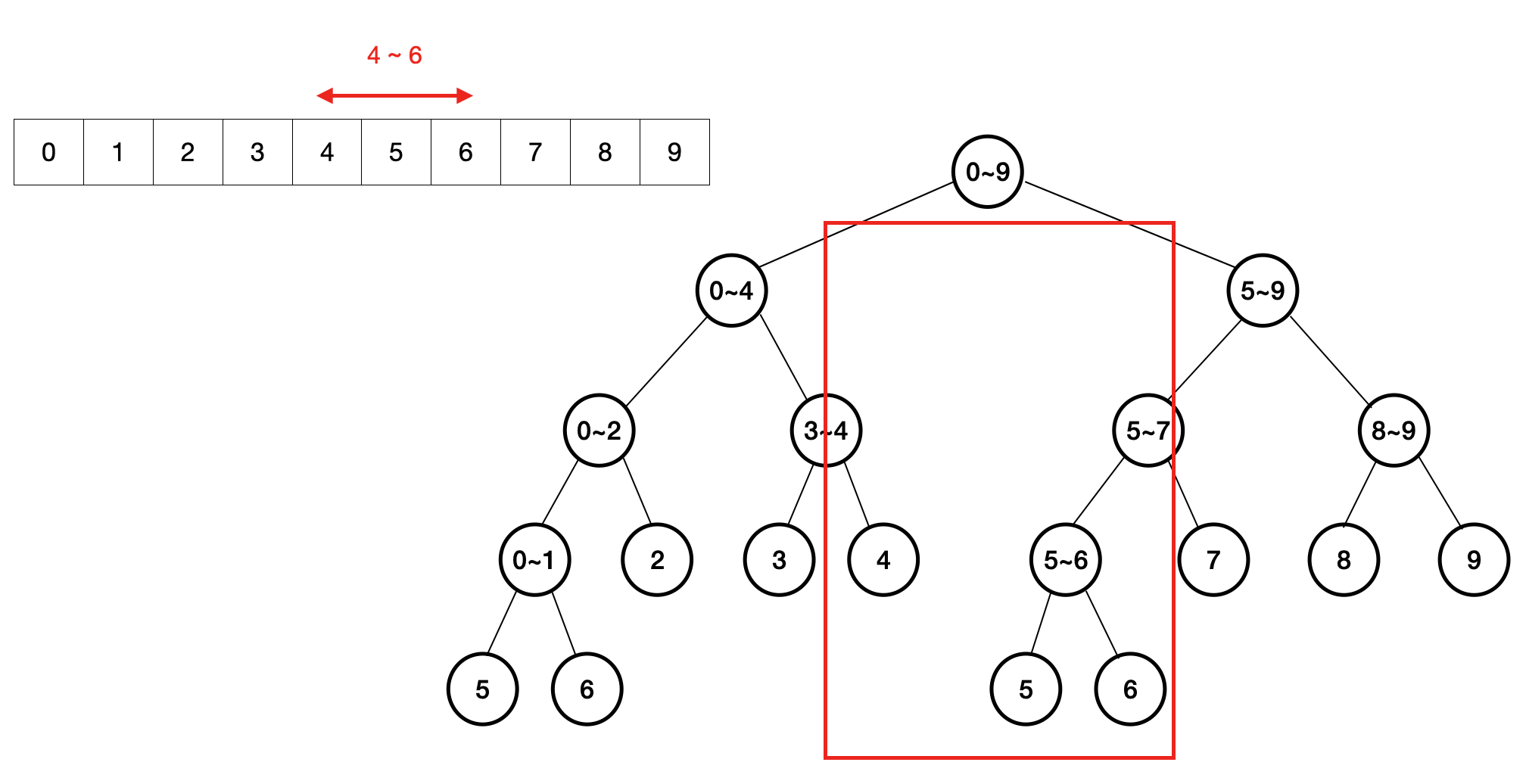
}

 

 

replace, 값 교체하기

이제 마지막으로 특정 인덱스의 값을 바꾸려고 합니다.

역시 재귀적 구현이 들어가는데요, 먼저 기저사례는 leaf 노드!  leftBounds == rightBounds 입니다.

아니라면, 기저사례까지 왼쪽이면 왼쪽의 자식으로, 오른쪽이면 오른쪽 자식으로 타고가서 값을 바꿔주고 

다시 왼쪽, 오른쪽을 연산해서 자신의 값도 바꿔주면 됩니다.

func replaceItem(at index: Int, withItem item: T) {
    if leftBounds == rightBounds {
        value = item
    } else if let leftChild = leftChild, let rightChild = rightChild {
        if leftChild.rightBounds >= index {
            leftChild.replaceItem(at: index, withItem: item)
        } else {
            rightChild.replaceItem(at: index, withItem: item)
        }
        value = function(leftChild.value, rightChild.value)
    }
}

 

전체 코드

최종 코드는 다음과 같습니다.

class SegmentTree<T> {
    var value: T
    var function: (T, T) -> T
    var leftBounds: Int
    var rightBounds: Int
    var leftChild: SegmentTree<T>?
    var rightChild: SegmentTree<T>?
    
    init(array: [T], leftBounds: Int, rightBounds: Int, function: @escaping (T, T) -> T) {
        self.leftBounds = leftBounds
        self.rightBounds = rightBounds
        self.function = function
        
        if leftBounds == rightBounds {
            self.value = array[leftBounds]
        } else {
            let middle = (leftBounds + rightBounds) / 2
            self.leftChild = SegmentTree<T>(
                array: array,
                leftBounds: leftBounds,
                rightBounds: middle,
                function: function
            )
            
            self.rightChild = SegmentTree<T>(
                array: array,
                leftBounds: middle+1,
                rightBounds: rightBounds,
                function: function
            )
            self.value = function(leftChild!.value, rightChild!.value)
        }
    }
    
    convenience init(array: [T], function: @escaping (T, T) -> T) {
        self.init(array: array, leftBounds: 0, rightBounds: array.count-1, function: function)
    }
    
    // O(logN)
    func query(withLeftBounds leftBounds: Int, rightBounds: Int) -> T {
        // left, right가 모두 일치 -> 자기 value 리턴
        if self.leftBounds == leftBounds, self.rightBounds == rightBounds {
            return value
        }
        
        guard let leftChild = leftChild,
              let rightChild = rightChild
        else { fatalError() }
        
        // 왼쪽자식의 오른쪽이 left보다 작다. -> 오른쪽 자식에 모두 포함되므로 오른쪽부터 다시
        if leftChild.rightBounds < leftBounds {
            return rightChild.query(withLeftBounds: leftBounds, rightBounds: rightBounds)
        }
        
        // 오른쪽자식의 왼쪽이 right보다 크다. -> 왼쪽 자식에 모두 포함되므로 왼쪽부터 다시
        else if rightChild.leftBounds > rightBounds {
            return leftChild.query(withLeftBounds: leftBounds, rightBounds: rightBounds)
        }
        
        // 양쪽 자식들에 걸쳐져 있음 -> (leftBounds ~ leftChild.right) + (rightChild.left ~ rightBounds)
        else {
            let leftValue = leftChild.query(withLeftBounds: leftBounds, rightBounds: leftChild.rightBounds)
            let rightValue = rightChild.query(withLeftBounds: rightChild.leftBounds, rightBounds: rightBounds)
            return function(leftValue, rightValue)
        }
    }
    
    // O(logN)
    func replaceItem(at index: Int, withItem item: T) {
        if leftBounds == rightBounds {
            value = item
        } else if let leftChild = leftChild, let rightChild = rightChild {
            if leftChild.rightBounds >= index {
                leftChild.replaceItem(at: index, withItem: item)
            } else {
                rightChild.replaceItem(at: index, withItem: item)
            }
            value = function(leftChild.value, rightChild.value)
        }
    }
}

let array = (1...10).map { $0 }
let segmentTree = SegmentTree<Int>(array: array, function: +)
segmentTree.query(withLeftBounds: 0, rightBounds: 9) // 55
segmentTree.replaceItem(at: 3, withItem: 10) // [1, 2, 3, 10, 4, 5, 6, 7, 8, 9, 10]

 

시간복잡도

SegmentTree는 이진트리로, query 도 replace도 O(logN) 의 연산으로 해결이 가능합니다.

 

이해하셨다면 이 문제도 한 번 풀어보세요!

세그먼트 트리만 구현되면 쉽게 푸실 수 있을거에요 :)

 

도움이 되셨다면 좋겠네요!

감사합니다 :)