합병정렬 Merge sort

목표

합병 정렬을 이해한다.
합병 정렬을 Swift로 구현한다.
합병 정렬의 시간 복잡도를 이해한다. ( O(nlogN) )
총 재귀 호출 횟수는 2n-1

 

합병 정렬 ?

합병 정렬은 분할정복 알고리즘의 하나입니다.

합병 정렬의 아이디어는

이미 정렬된 두 배열이 있다면 각 배열의 첫번째 원소끼리 비교해 정렬된 새로운 배열을 만들 수 있다.

에서 시작합니다. 

이 정렬된 두 배열을 얻기 위해 일단 최대한 작게 쪼개고 다 쪼갰다면, 
위의 아이디어를 이용해 정렬된 새로운 배열을 만들어 나가는 것이죠.

구체적으로 아래와 같은 과정을 거치게 됩니다.

1. 길이가 1 이하인 리스트는 정렬된 것으로 본다.
2. 분할(divide): 길이가 2이상이면 리스트는 반으로 쪼갠다.
3. 정복(conquer): 분할된 각 부분의 리스트를 정렬한다. ( 길이가 1이 될 때까지 쪼갠다. )
4. 병합(combine): 두 부분의 리스트를 정렬된 하나의 리스트로 병합한다.

출처: wikipedia

 

병합 방법

두 리스트를 병합할 때는 각 리스트의 첫번째 요소를 비교하면서 더 작은 원소를 임시 배열에 추가합니다.

 

구현

구현은 탑다운 방식과 바텀업 방식을 이용할 수 있습니다.

둘의 시간 복잡도는 동일하지만 분할하는 방법에 차이가 있습니다.

탑다운은 재귀를 이용해 리스트가 1이 될 때까지 반으로 계속 쪼개나가는 방법이고

바텀업은 1개씩 정렬, 2개씩 정렬, 4개씩 정렬을 반복해나가는 방법입니다.

 

탑다운 방식

func mergeSort(_ array: [Int]) -> [Int] {
    guard array.count > 1 else { return array }
    
    let mid = array.count/2
    let leftArray = mergeSort(Array(array[0..<mid]))
    let rightArray = mergeSort(Array(array[mid..<array.count]))
    
    return merge(leftPile: leftArray, rightPile: rightArray)
}

func merge(leftPile: [Int], rightPile: [Int]) -> [Int] {
    var leftIndex = 0
    var rightIndex = 0
    
    var orderedPile = [Int]()
    
    while leftIndex < leftPile.count, rightIndex < rightPile.count {
        
        if leftPile[leftIndex] <= rightPile[rightIndex] {
            orderedPile.append(leftPile[leftIndex])
            leftIndex += 1
        } else {
            orderedPile.append(rightPile[rightIndex])
            rightIndex += 1
        }
    }
    
    while leftIndex < leftPile.count {
        orderedPile.append(leftPile[leftIndex])
        leftIndex += 1
    }
    
    while rightIndex < rightPile.count {
        orderedPile.append(rightPile[rightIndex])
        rightIndex += 1
    }
    
    return orderedPile
}

 

바텀업 방식

func mergeBottomUp(_ array: [Int]) -> [Int] {
    
    var size = 1
    var orderedArray = array
    
    while size  < array.count {
        var i = 0
        while i < array.count {
            var pileIndex = 0
            
            let max = min(i + size * 2, array.count)
            let mid = min(i + size, max)

            let leftPile = Array(orderedArray[i..<mid])
            let rightPile = Array(orderedArray[mid..<max])
            let orderedPile =  merge(leftPile: leftPile, rightPile: rightPile)

            
            while pileIndex < orderedPile.count {
                orderedArray[pileIndex+i] = orderedPile[pileIndex]
                pileIndex += 1
            }
            
            i = max
        }
        
        size *= 2
    }
    
    return orderedArray
}


func merge(leftPile: [Int], rightPile: [Int]) -> [Int] {
    var leftIndex = 0
    var rightIndex = 0
    
    var orderedPile = [Int]()

    while leftIndex < leftPile.count, rightIndex < rightPile.count {
        if leftPile[leftIndex] <= rightPile[rightIndex] {
            orderedPile.append(leftPile[leftIndex])
            leftIndex += 1
        } else {
            orderedPile.append(rightPile[rightIndex])
            rightIndex += 1
        }
    }
    
    while leftIndex < leftPile.count {
        orderedPile.append(leftPile[leftIndex])
        leftIndex += 1
    }
    
    while rightIndex < rightPile.count {
        orderedPile.append(rightPile[rightIndex])
        rightIndex += 1
    }

    return orderedPile
}

 

시간복잡도

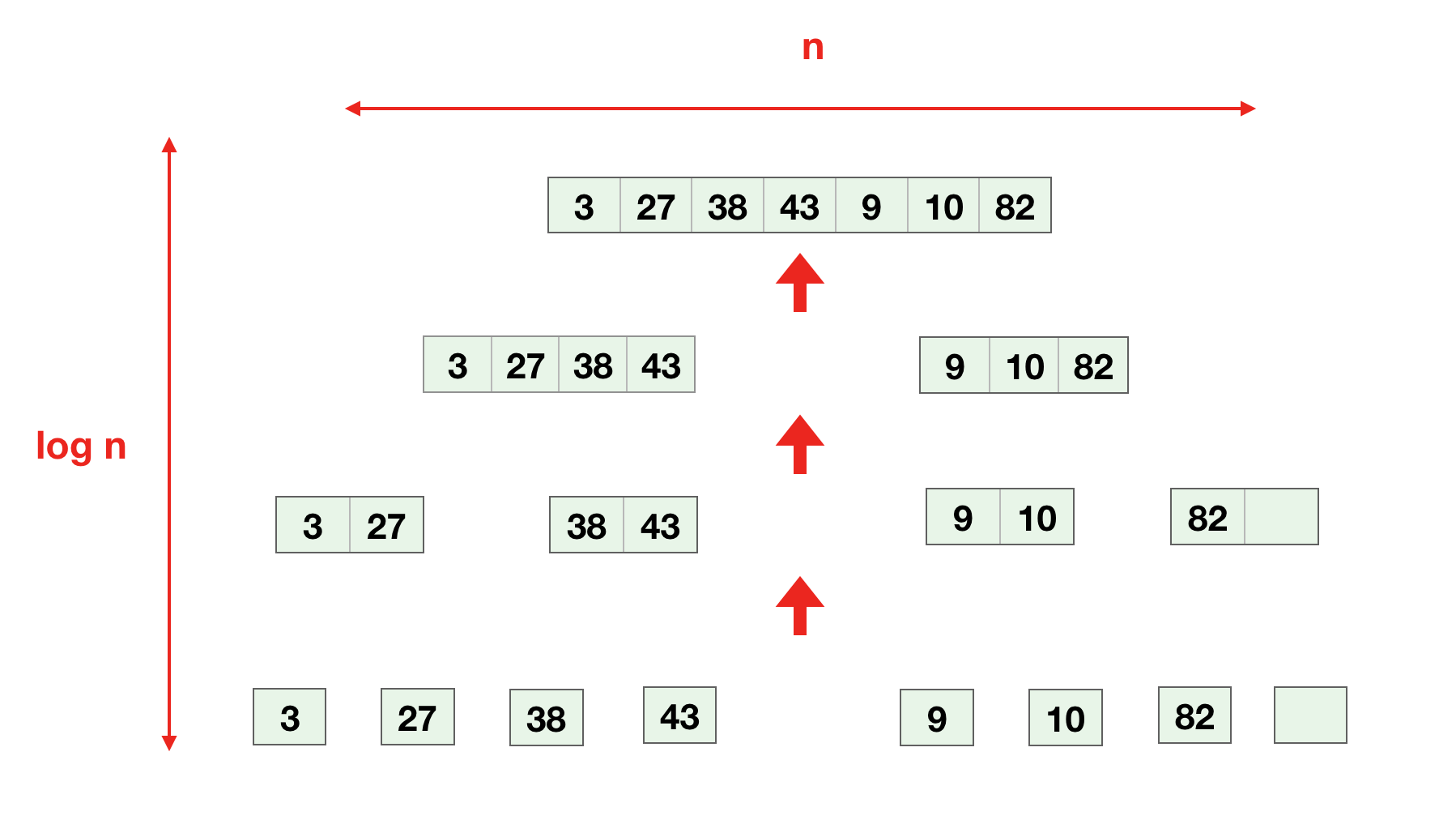
분할정복의 시간복잡도는 n log n 입니다.

n 개를 1개로 쪼개려면 log n 만큼의 과정이 필요합니다.

그리고 그게 n개 있으니 n * log n 해서 n log n 이 됩니다.

예를 들어, 8을 반씩 쪼개서 1로 만들려면 3번을 쪼개야겠죠? 이게 log n 입니다.
그리고 1로 쪼개진 배열은 8개, n만큼이 생기겠죠?
그래서 결과적으로 n만큼 log n 번이 호출되게 됩니다.

이런식으로 보면 좀 더 이해가 쉬울까요?

합병정렬은 물리적으로 반을 나누기 때문에 최악의 경우에도 n log n 의 시간복잡도를 갖습니다. :)

 

감사합니다.