위상정렬 Topological Sort

목표

- 위상정렬 (Topological Sort)를 이해하고 설명할 수 있다.
- 위상정렬의 조건을 알고 언제 어떻게 사용하는지 이해한다.

 

---

 

위상정렬?

\

특정한 순서를 가진 조건에서 사용한다.

DAG(방향성 비순환 그래프) 에서만 사용할 수 있다.

\

 

 

"위상" 이라는 사전적 정의에서 알 수 있듯이, 위상정렬이란 어떤 순서를 가지고 있는 경우에 사용할 수 있는 정렬 방법입니다.

게임을 하는데 어떤 스킬을 익히기 위해 반드시 먼저 배워야 하는 사전스킬이 있죠? 이런 식으로 어떤 순서를 가지고 있을 때 사용합니다.

이 말인즉 위상정렬은 방향성을 가지고 있어야 합니다. 그리고 이 의미를 잘 생각해보면 사이클이 생기면 안된다는 것을 알 수 있습니다. 

A -> B -> C 순서를 가지고 있어야 하는데 여기서 C -> A가 되어버린다면? 말이 안되겠죠?

방향성을 가지고 사이클이 없는 그래프를 DAG(Directed Acyclic Graph) 방향성 비순환 그래프라고 합니다.

 

구현

위상정렬은 다음 방식으로 진행됩니다.

\

1. 진입차수가 0인 노드를 큐에 담는다.

2. 큐에서 노드를 꺼내고 해당 노드에 연결된 간선을 모두 제거한다.

3. 다시 진입차수가 0인 노드를 큐에 담는다.

4. 큐에서 꺼낸 순서가 정렬 순서가 된다.

\

 

위상정렬은 스택이나 큐를 사용해서 구현할 수 있는데요, 오늘은 큐를 사용해서 구현해보려고 합니다.

진입차수라는 개념이 등장하는데요, 이는 자신으로 향하는 화살표의 개수를 의미합니다. 

진입차수가 없다는 말은 바로 접근할 수 있다는 의미가 되겠죠. 진입차수가 없는 것부터 시작해서 간선을 끊어내면서 정렬해나가는 방식이라고 할 수 있습니다.

 

다음과 같은 그래프를 생각해봅시다. 
각 노드의 진입차수를 계산해보면, 아래와 같고 큐에 진입차수가 0인 1을 큐에 담습니다.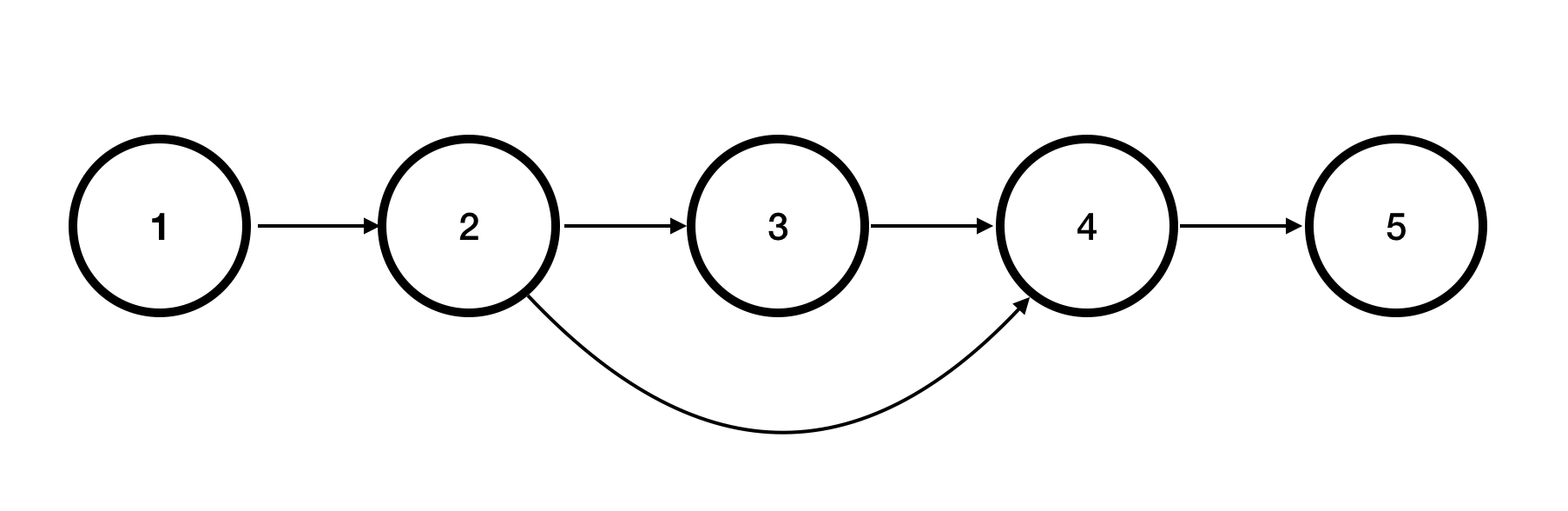

노드	1	2	3	4	5
진입차수	0	1	1	2	1
Queue	1
결과

 

다음으로 큐에 하나를 꺼내고 꺼낸 노드에 연결된 간선을 모두 제거합니다.
그리고 다시 진입차수가 0인 노드 2를 큐가 담습니다. 

 

노드	1	2	3	4	5
진입차수		0	1	2	1
Queue	2
결과	1

 

다시 2를 꺼내고 2에 연결된 간선을 모두 제거하고 진입차수가 0인 3을 큐에 담습니다.
2에서 4로 가고 있었던 간선도 제거했으니 4의 진입차수는 1이 되겠죠?

 

노드	1	2	3	4	5
진입차수			0	1	1
Queue	3
결과	1, 2

 

 

이렇게 반복해나가면 됩니다.

정상적인 위상정렬이라면 딱 N번만 실행되어야 합니다. 

아직 정렬이 끝나지 않았는데 큐가 비어있다면 사이클이 생겼다는 의미가 됩니다. 이때는 위상정렬을 할 수 없습니다.

 

이제 코드로 직접 살펴보겠습니다.

처음 맨 처음에 진입 차수가 0인 노드를 확인해 큐에 담아 시작하고, 간선을 제거하고 나서 간선이 제거된 노드의 진입차수가 0인지 확인하면서 큐에 담는 방식으로 구현합니다.

편의상 Graph 구조체를 정의해서 사용했습니다.

struct Graph<T>: Equatable where T: Equatable {
    var childs: [T]
    
    mutating func push(_ child: T) {
        self.childs.append(child)
    }
}

var n = 5
var inDegree = [Int](repeating: 0, count: n) // 각 정점의 진입차수 정보
var trees = [Graph<Int>]()

func topologicalSort() -> [Int] {
    // 결과를 담을 배열과 queue가 필요하다.
    var result = [Int]()
    var q = [Int]()
    
    // 진입차수가 0인 노드를 큐에 담는다.
    for i in 0..<n {
        print(i)
        if inDegree[i] == 0 { q.append(inDegree[i]) }
    }
    
    // 위상정렬은 총 n 번만 실행되어야 한다.
    for _ in 0..<n {
        
        // 큐가 비어있으면 사이클이 생긴 것이다.
        if q.isEmpty {
            print("사이클이 생겨버렸어요 ⁉️")
            return
        }
        
        // 큐에서 노드를 하나 꺼내고 인접 간선을 모두 제거한다.
        // 진입차수가 0인 노드를 큐에 담고를 반복한다.
        result.append(q.first!) // 위에서 확인하고 왔으므로 큐가 비어있지 않음이 보장된다.
        let node = q.removeFirst()
        
        for child in trees[node].childs {
            inDegree[child] -= 1
            if inDegree[child] == 0 {
                // 새롭게 진입차수가 0 이 된 노드를 큐에 삽입한다.
                q.append(child)
            }
        }
    }
    
    return result
}

 

시간복잡도

마지막으로 위상정렬의 시간복잡도는 O(V + E) 입니다.

앞서 잠깐 말씀드렸다시피 위상정렬은 딱 N번만 실행(V)되어야 합니다. 그리고 각 횟수에 간선을 모두 끊어내는 작업(E)이 들어가죠.

따라서 O(V+E) 만으로 해결할 수 있습니다. 위상정렬을 사용할 수 있는 조건만 갖춰진다면 매우 빠른 강력한 알고리즘입니다.

 

긴 글 읽어주셔서 감사합니다 :)